渐变虽是一种变化，但在变化过程中具有本质联系和必然趋势 --- 规律。这种规律往往以数列等形式实现。

1、等差数列
如果数列从第二项开始，每一项与前一项的差为常数d，则称为“等差数列”。d称为“公差”。等差数列可以写成a, a+d......, a+nd,··…的形式(下图l~4)。
 
2、等比数列
如果数列从第二项开始，每一项与前一项的比为常数r，则称为“等比数列”，r为“公比”。等比数列可以写成a, ar,……，ar的n次方，……的形式(下图1, 2)。

3、费波纳奇数列
费波纳奇数列为0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.....即每一项都是前两项之和(下图3)。

 4、贝尔数列
贝尔数列为0,1, 2, 5, 12, 29, 70, 169"···，即每一项都是前项的2倍并再与再前项相加(下图4）。

5、平方根矩形
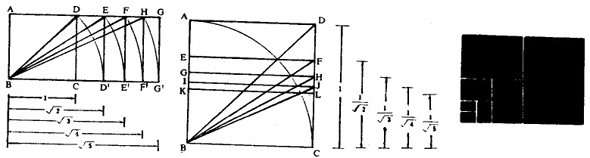
长边和短边之比构成平方根的矩形称之为平方根矩形，下图1, 2为平方根矩形作图法及渐变状态。

在平方根矩形中，短边为1，长边为根号下2的矩形叫根号下2矩形。根号下2矩形的特点是，偶数均分后的矩形，其长短边之比仍是根号下2，这可以从下图3根号下2矩形的商标中得到验证。

6、阿基米德螺线
亦称“等速螺线”。当一点P沿动射线OP以等速运动的同时，该射线又以等角速度线点O旋转，点P的轨迹称为“阿基米德螺线”(下图1)。阿基米德螺线以其优美的节奏和旋律在螺线布局中应用最广(下图2)。
下图3从中心开始，扇形由小到大逆时针排列，其顶角连线为阿基米德螺线。下图4亦从中心开始，弧线长度由短至长，弧度由小至大，顺时针按阿基米德螺线排列。

在用数列等形式确定其规律时，邻项差异不要太大，以免“反差”过重;项数也不要太多，以免拥挤。总之，对邻项差异和项数要综合考虑，力求使渐变式标志疏密得当。
 

阅读渐变标志的规律的还阅读了：渐变标志的构成